(1)例題
①硬貨2枚を同時に投げる。少なくとも1枚は表であるとき、2枚とも表である確率を求めよ。
②赤玉3個、白玉2個、黒玉1個が入っている袋から、玉を1個取り出し、それをもとに戻さないで、続いてもう1個取り出す。1回目に赤玉が出たとき、2回目も赤玉が出る確率を求めよ。
(2)例題の答案
①
少なくとも1枚は表が出るという事象をA、2枚とも表が出るという事象をBとする。
硬貨2枚の裏表の全事象は、
(表、表)(表、裏)(裏、表)(裏、裏)
であるので、
P(A)=3/4, P(A∩B)=1/4 となる。
よって、
PA(B)=P(A∩B)÷P(A)=1/3
②
1回目に赤玉を取り出すという事象をA、2回目に赤玉を取り出すという事象をBとする。
P(A)=1/2
P(A∩B)=1/2×2/5=1/5
よって、
PA(B)=P(A∩B)÷P(A)=2/5
(3)解法のポイント
条件付き確率は公式通りに求めましょう。
①Aとなる確率を求める(分母)
②A∩Bとなる確率を求める(分子)
の順番で1つずつ求めるとよいでしょう。
そして、②÷①をすれば答えです。
また、問題によっては①を求める過程の場合分けで②が出てくることもあります。
(4)必要な知識
①条件付き確率の公式
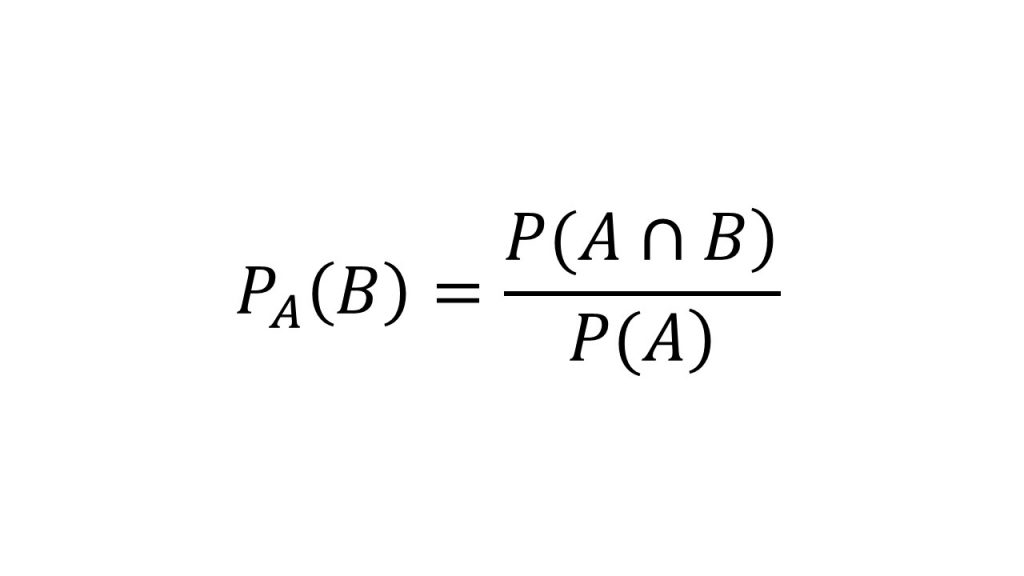
※PA(B)は「AのときのBの確率」と読む。P(A∩B)は「AかつBの確率」と読む。
(5)解説授業
①条件付き確率の原理を解説します!(条件付き確率の公式、条件付き確率が意味すること、条件付き確率の求め方の流れについても解説します)
