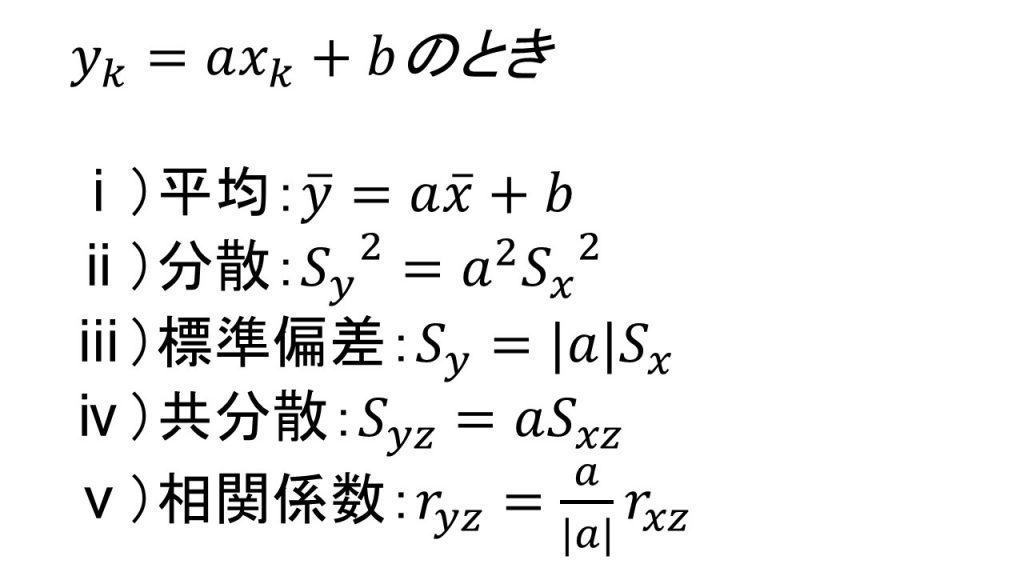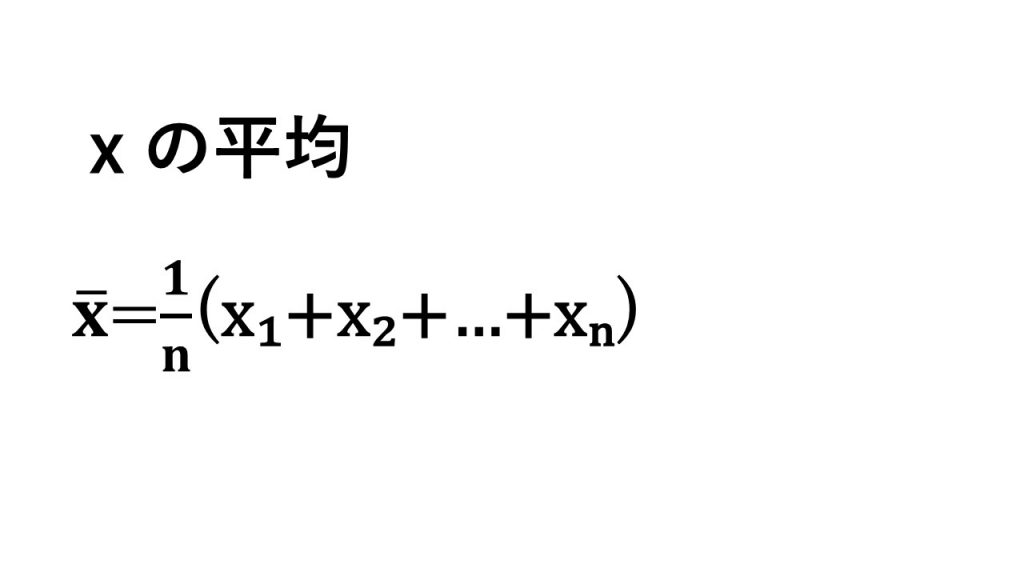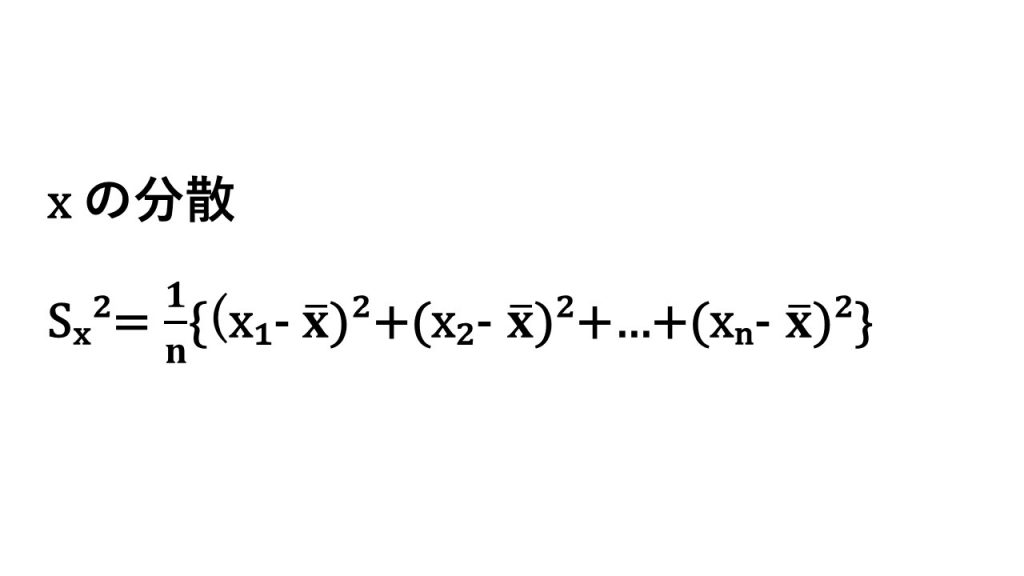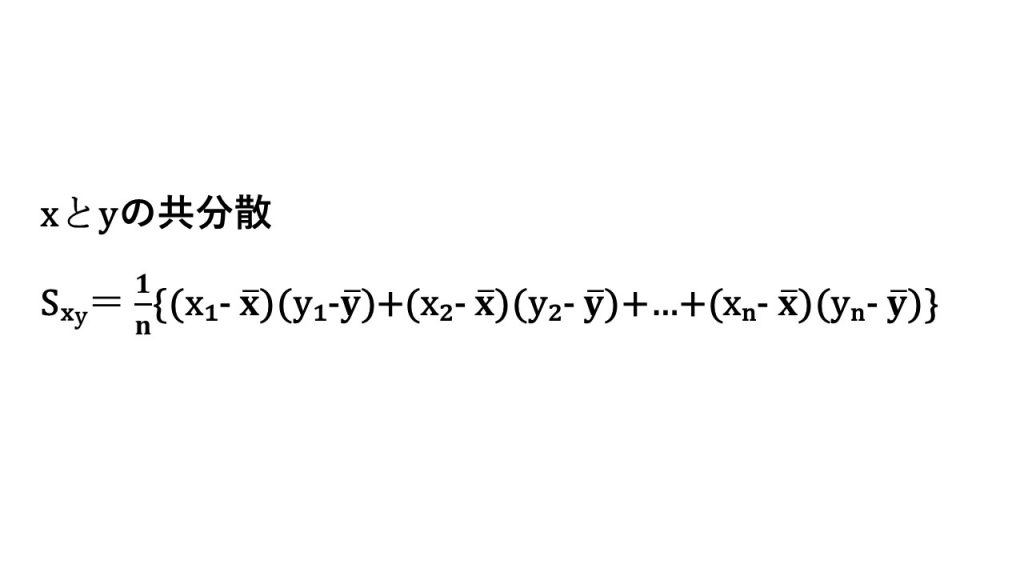(1)例題
以下の【①】~【③】に当てはまる数字を答えよ。
N市では温度の単位として摂氏(℃)のほかに華氏(°F)も使われている。華氏(°F)での温度は、摂氏(℃)での温度を9/5倍し, 32を加えると得られる。例えば、摂氏 10℃は、9/5倍し、32を加えることで華氏50 °Fとなる。
したがって、N市の最高気温について、摂氏での分散をX、 華氏での分散をYとすると、YはXの【①】倍になる。
東京(摂氏)とN市(摂氏)の共分散をZ、東京(摂氏)とN市(華氏)の共分散をWとすると、WはZの【②】倍になる。
東京(摂氏)とN市(摂氏)の相関係数をU、東京(摂氏)とN市(華氏)の相関係数をVとすると、UはVの【③】倍になる。
(センター試験2016年本試数学ⅠA第2問〔3〕(3)より)
(2)例題の答案
①

②

③
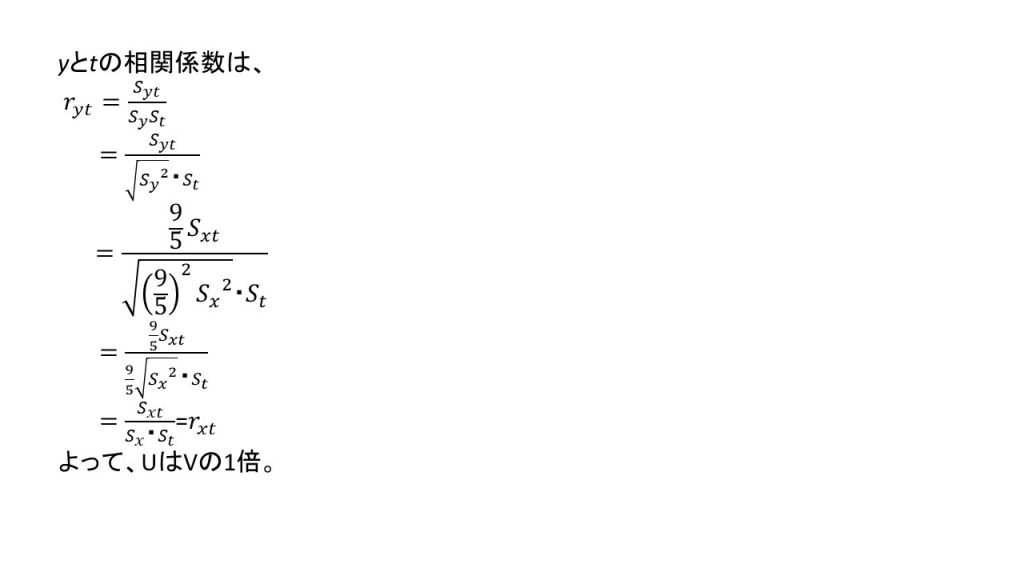
(3)解法のポイント
定義から理解することが大切です。
変量を変換したとき、ⅰ)平均、ⅱ)分散、ⅲ)標準偏差、ⅳ)共分散、ⅴ)相関係数がそれぞれどう変化するか、定義を使って証明してみます。
ⅰ)平均

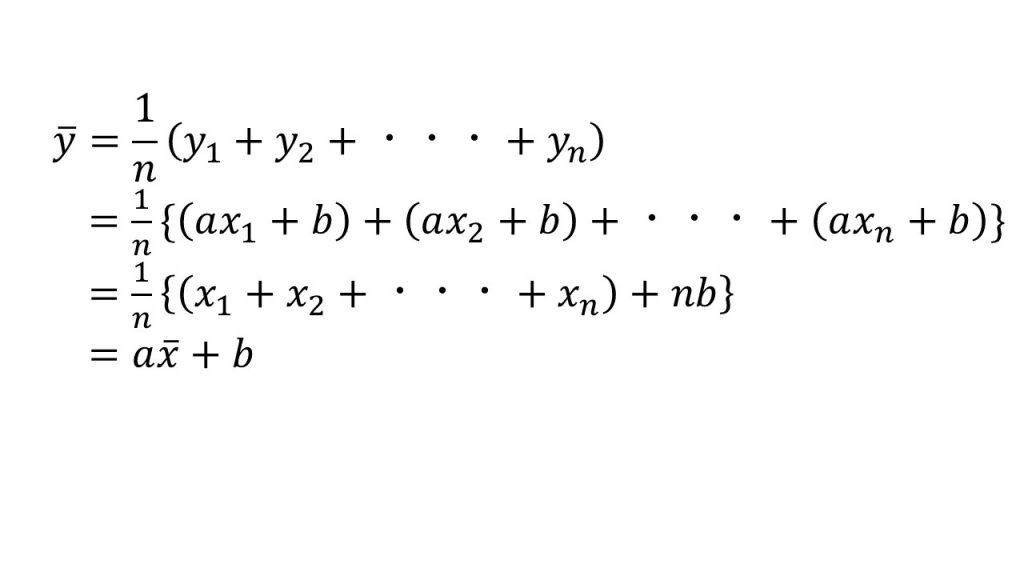
☆受験生はΣを使って書けるようになろう。
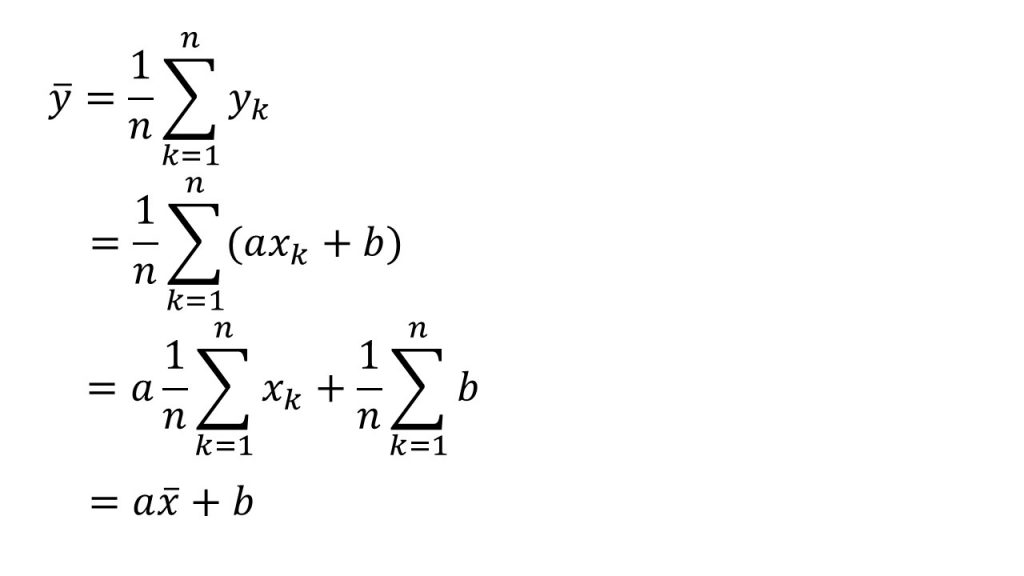
ⅱ)分散

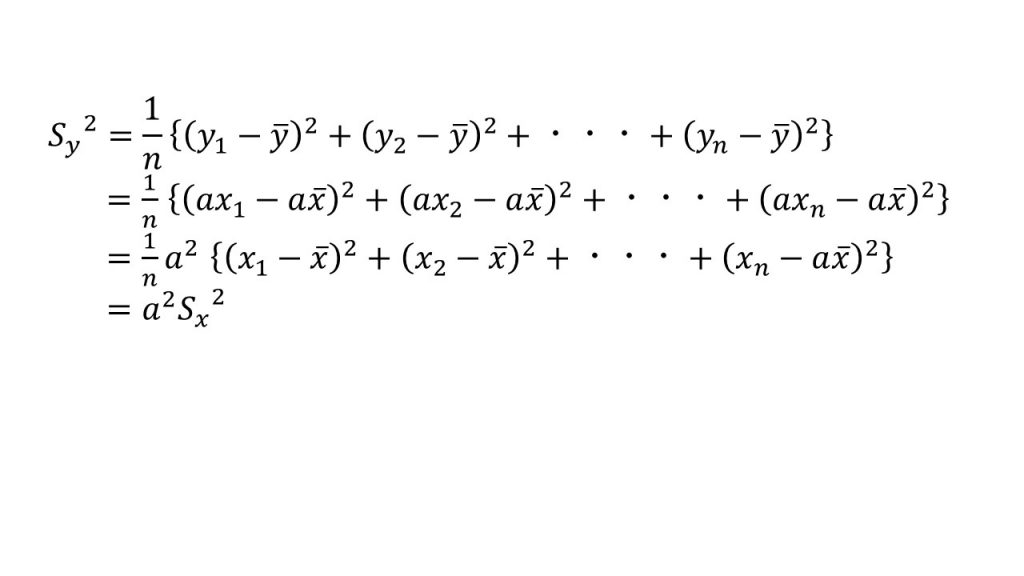
☆受験生はΣを使って書けるようになろう。
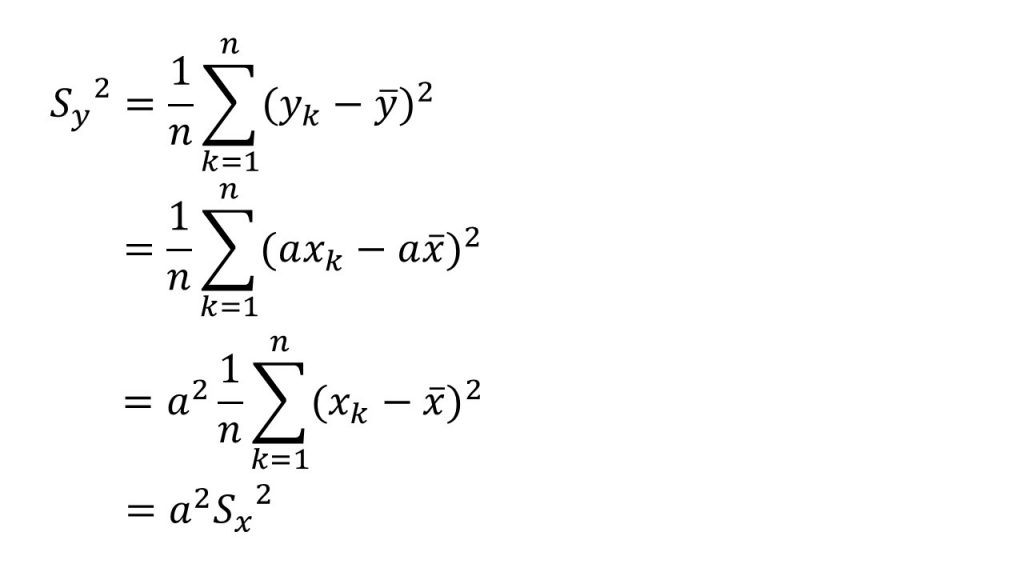
ⅲ)標準偏差

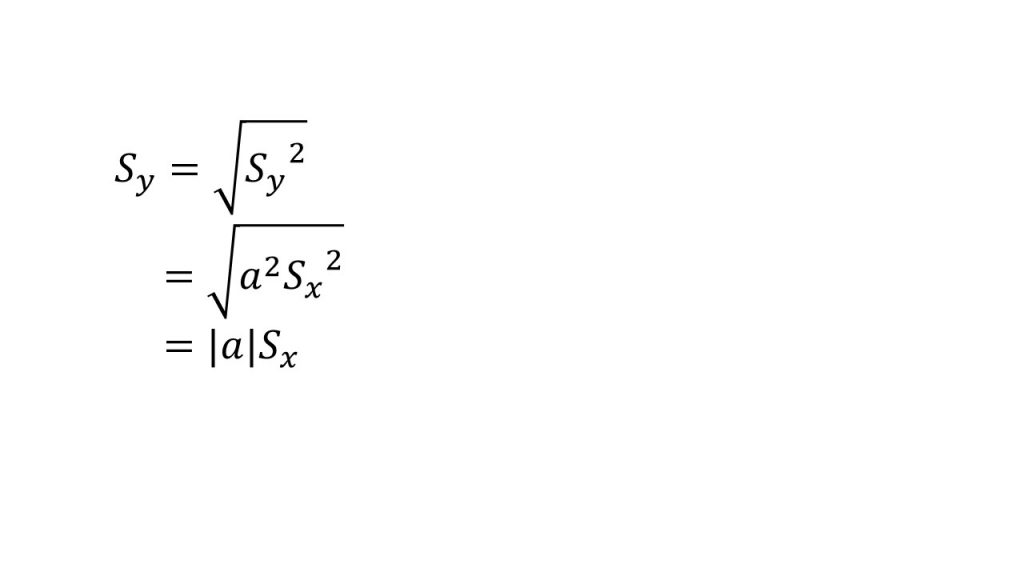
ⅳ)共分散

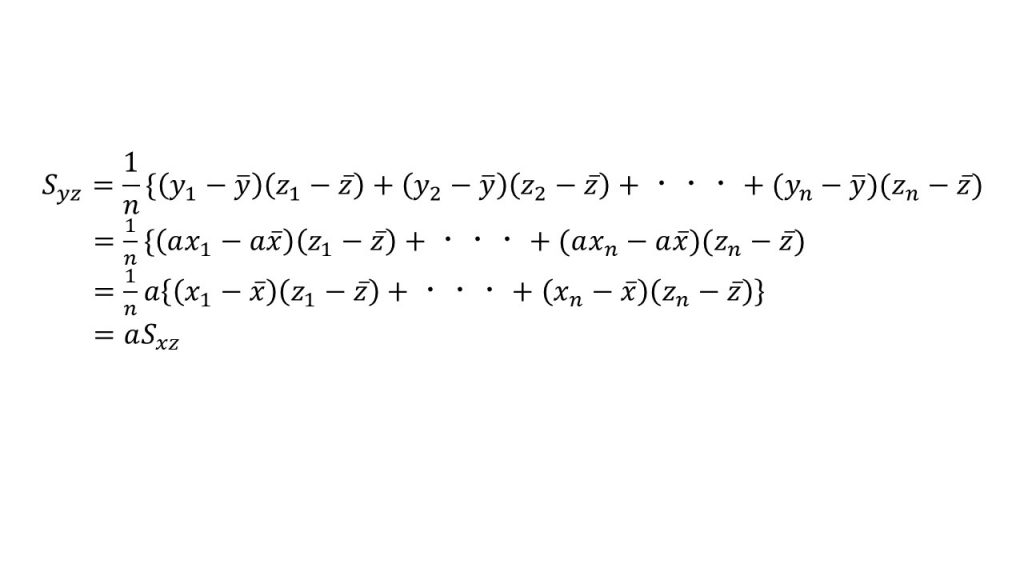
☆受験生はΣを使って書けるようになろう。
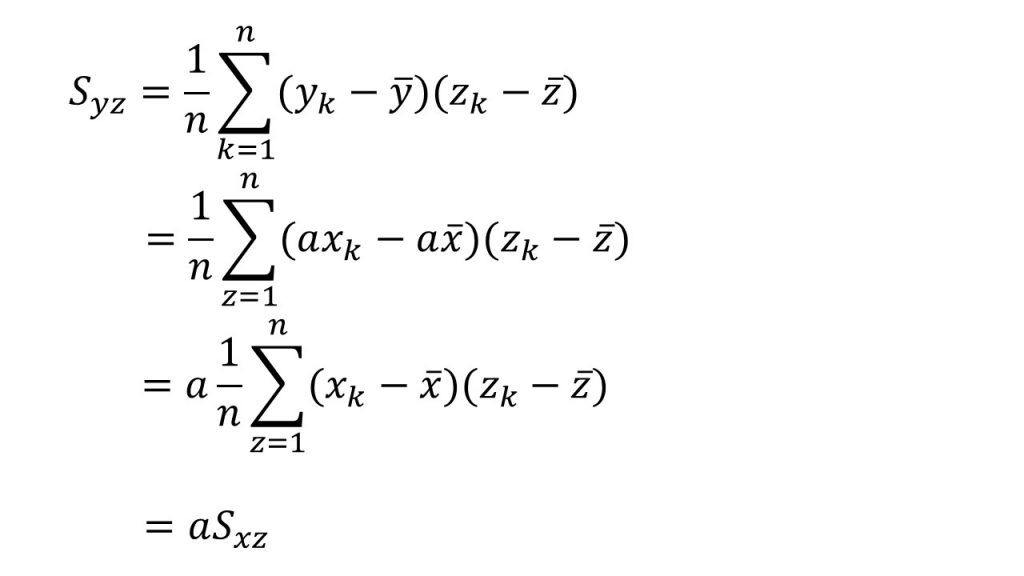
ⅴ)相関係数

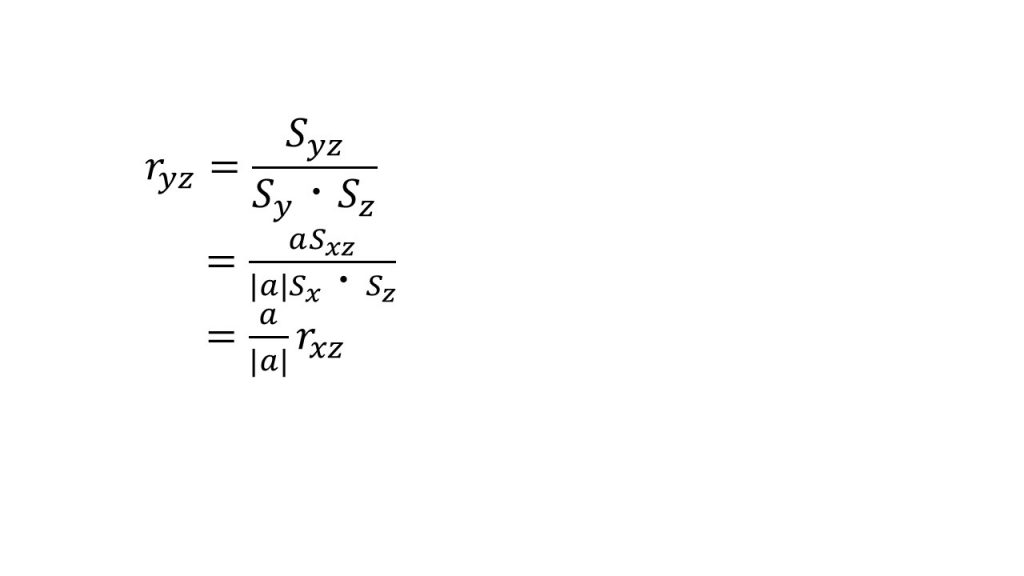
(4)必要な知識