(1)例題
①aaabbcを1列に並べる並べ方を求めよ。
②1から4までの数字を、重複を許して並べてできる4桁の自然数のうち、1331のように異なる2つの数字を2回ずつ使ってできるものの個数を求めよ。
(2013年センター試験本試数学ⅠA第4問(3)より)
(2)例題の答案
①6!÷3!÷2!=60通り
②
(ⅰ)4つの数字から異なる2つを選ぶ選び方は
4C2=6通り
(ⅱ)ⅰで選んだ数字を1列に並べる並べ方は〇〇□□の順列と考えると、
4!/2!2!=6通り
よって、求める個数は
6×6=36個
(3)解法のポイント
同じものを含む順列を考える問題は、まず全て区別できるとして並べた後、
(同じものの数)!
で割ります。
例えば、aaabbcの順列であれば、
6!÷3!÷2!
です(6!は6つの文字が全て区別できるとして並べたときの並べ方、3!はaが3つかぶっているということ、2!はbが2つかぶっているということ)
(4)必要な知識
①同じものを含む順列

②Cの定義
→n個のうちからr個選ぶときの選び方
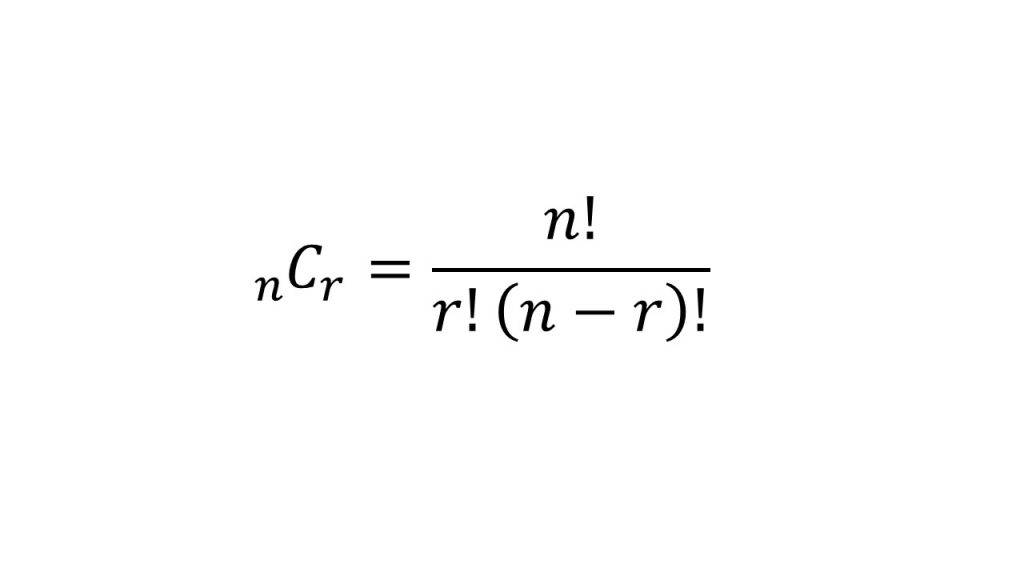
(5)理解すべきこと
同じものを含む順列の原理を理解しましょう→同じものを含む順列の原理(なぜ同じものの階乗で割るのか、最短経路)
☆動画はこちら↓
